У дослідженнях моделювання подій ви можете вказати, на яку відстань має рухатися тіло чи об’єкт, напрямок, у якому воно має рухатися, і швидкість його руху. Цей заданий рух здійснюється шляхом застосування встановлених обмежень руху або перехідних навантажень і визначення величини та напрямку. Спосіб, у який відбувається зміщення, визначається за допомогою кроків на кривій множника або кривій величини .

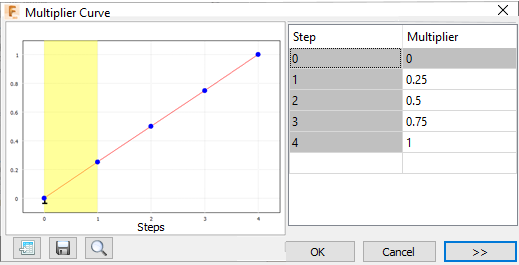
Малюнок 1. Приклад кривої множника, що показує непотрібні проміжні кроки.

Криві з різною кількістю кроків

Ви можете створити іншу криву для кожного заданого обмеження або перехідного навантаження, яке ви встановили, і кожна крива може мати різну кількість кроків.

Якщо дослідження містить кілька кривих із різною кількістю кроків, симуляція події використовує найбільшу кількість кроків для визначення аналізу. Для кожної кривої, яка передбачає меншу кількість кроків, останній крок подовжується лінійно, так що він закінчується узгоджено з кривою з найбільшою кількістю кроків.

Приклад 1. Різні криві, однакова швидкість переміщення :

На перший погляд дві криві, показані на малюнку 2, здається, що визначають різні швидкості переміщення. Однак, коли вони використовуються спільно в одному дослідженні, криві визначають однакову швидкість зміщення.

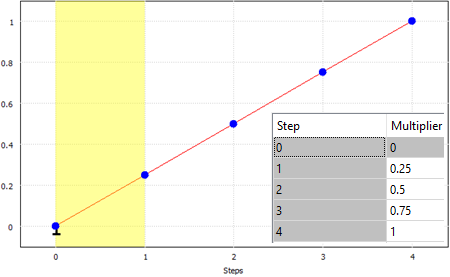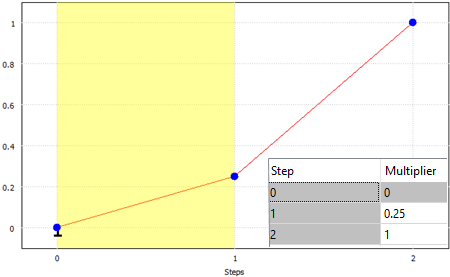
Рисунок 2(a) 2-крокова крива мультиплікатора. Насправді 2-й крок подовжений, щоб відповідати 2(b)	Рисунок 2(b) 4-крокова крива множника. Ця крива контролює форму кривої в 2(a)

На малюнку 2 обидві криві визначають множник 0,25 при переході від 0 до кроку 1. На кроці 2 крива на малюнку 2(a) визначає перехід від множника 0,25 до повного зміщення лінійним чином. Між тим, малюнок 2(b) також визначає лінійний перехід від множника 0,25 до повного об’єму, але використовує додаткові кроки. Результатом є те, що обидві криві визначають однакове зміщення.

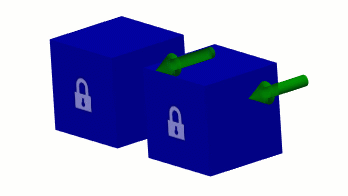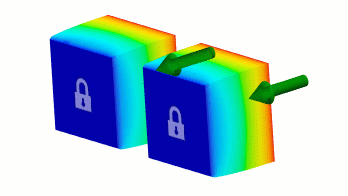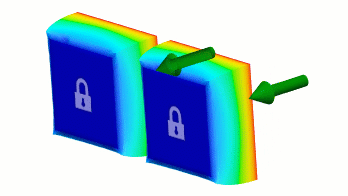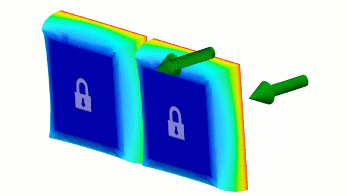Малюнок 3 Криві з різними кроками, що визначають однакову швидкість переміщення.

Приклад 2. Різні криві, різні швидкості переміщення :

Дві криві, показані на малюнку 4, мають різну кількість кроків І визначають різні швидкості переміщення. Незважаючи на очевидну форму кривих, на малюнку 4(a) показана більш висока швидкість переміщення на першому кроці.

Крива на малюнку 4(a) визначає перехід на кроці 1 від 0 до 0,5 множника повного об’єму. Тим часом крива, визначена на малюнку 4(b), визначає перехід від 0 до 0,25 множника повного об’єму. У результаті після кроку 1 ліве тіло відхилилося далі, ніж праве тіло.

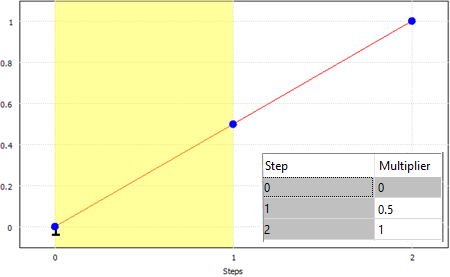Рисунок 4(a) 2-крокова крива мультиплікатора. Насправді 2-й крок подовжений, щоб відповідати 4(b)	Рисунок 4(b) 4-крокова крива множника. Ця крива керує формою кривої в 4(a)

Потім крива на малюнку 4(a) визначає лінійне відхилення від множника 0,5 до повного відхилення протягом решти тривалості. Крива на малюнку 4(b) також визначає лінійний перехід до повного відхилення протягом решти часу, але він починається з 0,25 множника повного відхилення. Оскільки обидві криві закінчуються в одній точці, результатом є те, що відхилення лівого тіла більше на першому кроці, але швидкість наступного відхилення більша в правому тілі, так що вони можуть завершитися тим самим відхиленням на тій же час.

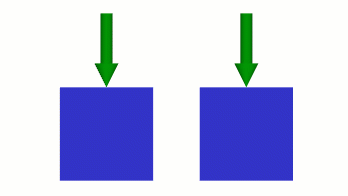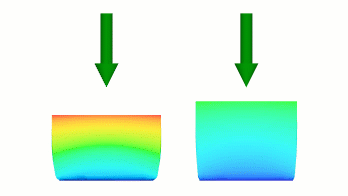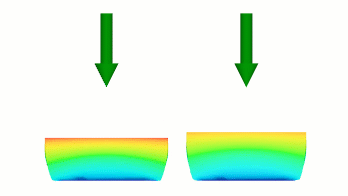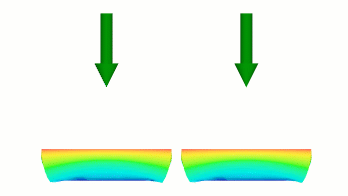Малюнок 5 Криві з різними кроками, що визначають різні швидкості переміщення.