Нелінійні характеристики напруження-деформації гіперпружних матеріалів, таких як гума, є складними. Чимало доступних сортів матеріалу дуже відрізняються за поведінкою. Для нелінійного моделювання у Fusion 360 гіперпружні матеріали представлені за допомогою 2-константної стандартної моделі матеріалу Муні-Рівліна . Коефіцієнти матеріалу виводяться на основі експериментально отриманих необроблених даних напруги та деформації. Ці дані можуть ґрунтуватися на різних випробуваннях, включаючи наступні приклади випробувань на розтягування/стиск:

• Одноосьовий (1 і 2)
• Площинний
• Рівнодвовісний
• Двовісний
• обмежений
• Триосьовий
• Об'ємний

Опис цих тестів і вихідних даних, які вони створюють, виходять за рамки цієї теми. Випробування матеріалів проводяться лабораторіями, які спеціалізуються на цьому процесі, а підгонку кривої потрібно виконувати за межами Fusion 360. (Програма не має вбудованого засобу для прийняття необроблених даних і виконання функції підгонки кривої.) Існують різні програми для виконання необхідної функції підгонки кривої після отримання необроблених даних. Однією з таких програм є HyperFit , яка доступна у безкоштовній демо-версії (з обмеженою функціональністю) та ліцензійній версії. Для створення кривої та результуючих констант матеріалу потрібна повна ліцензія.

Модель гіперпружного матеріалу Муні-Рівліна

Гіперпружні матеріали у Fusion 360 моделюються за допомогою 2-константної стандартної моделі матеріалу Муні-Рівліна. Використовується формула, що майже не стискується, тому об’ємні терміни включені у функцію енергії деформації. Ефекти деформації зсуву та об’ємної деформації розділені.

Загальна функція енергії деформації Муні-Рівліна

Зв’язок між енергією деформації, деформацією зсуву та об’ємною деформацією виражається наступною функцією загального випадку (застосовна до випадків 2-постійних і вищих порядків):

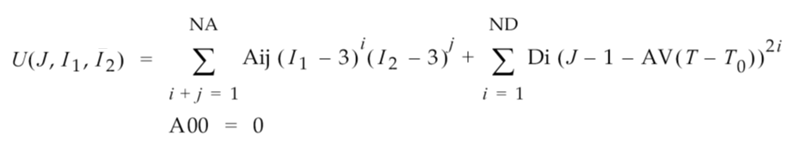
Де:

• U – енергія деформації.
• I1 є першим інваріантом деформації спотворення.
• I2 є другим інваріантом деформації спотворення.
• J = det F , що є детермінантом градієнта деформації.
• Aij — це набір констант матеріалу, пов’язаних із деформацією зсуву (i та j є індексами окремих констант).
• Di — набір констант матеріалу, пов’язаних з об’ємною деформацією.
• AV – об’ємний коефіцієнт теплового розширення.
• Т – поточна температура
• T0 – початкова температура

Спрощене 2-константне рівняння Муні-Рівліна

Наразі Fusion 360 не підтримує термічні ефекти для гіперпружних матеріалів у нелінійному аналізі. Таким чином, ми можемо спростити попередню функцію, виключивши члени теплового розширення (AV, T і T0) і обробивши суму для констант, які приймає Fusion 360 (A01, A10 і D1). Тоді спрощене рівняння енергії деформації стає таким:

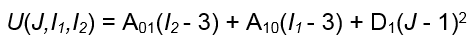
Де:

• *U , J , I1* і I2 мають значення, визначені раніше.
• A01 є першою з двох констант викривлення, пов’язаних із деформацією матеріалу при зсуві .
• A10 є другою з двох констант викривлення, пов’язаних із деформацією матеріалу при зсуві .
• D1 — константа, пов’язана з об’ємною деформацією матеріалу, яка дорівнює половині об’ємного модуля (К).

Тобто 2D1 = K. Отже, D1 = K/2