Симуляція події 01
Пластична деформація товстої порожнистої кулі внутрішнім тиском.
Опис справи
Цей приклад перевірки точності демонструє надійність розв’язувача моделювання подій у кількісному визначенні таких трьох явищ:
- Залежні від часу прикладені навантаження
- Нелінійна поведінка матеріалу, зокрема пластична деформація при навантаженні понад текучість
- Використання симетрії для визначення поведінки повного тіла, використовуючи лише часткове, набагато менше, представлення
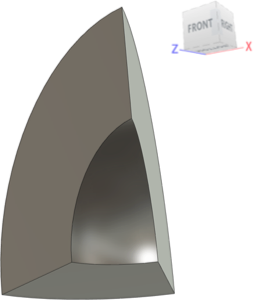
Модель є представленням товстостінної порожнистої кулі симетрією однієї шістнадцятої. Рівномірний тиск на внутрішню поверхню порожнини. Величина тиску лінійно зростає. У якийсь момент події на внутрішній поверхні починає відбуватися пластична деформація. У міру того, як симуляція події триває, більша частина товщини стінки поступово досягає рівня пластичного напруження. Згодом зовнішня поверхня досягає межі текучості, після чого сфера починає швидко розширюватися. Розрахунок тиску, необхідного для досягнення пластичного стану на внутрішній і зовнішній поверхнях, показано на цій сторінці. Результати Fusion 360 порівнюються з теоретичними результатами.
Передбачається ідеально пластичний матеріал, що означає, що нахил кривої напруження-деформації є плоским (нульовим) після досягнення текучості. Іншими словами, зміцнення матеріалу не відбувається. Це припущення спрощує теоретичне виведення.
Обмеження без тертя представляють умови симетрії на кожній розрізаній (плоскій) поверхні порожнистої сфери.
Тип дослідження та параметри
- Симуляція подій
- Загальна тривалість події = 0,051 секунди
- Кількість інтервалів збереження результатів = 51 (один набір результатів на мілісекунду)
- Критерії видалення елемента: не встановлено
Геометрія моделі
- Опис: одна шістнадцята порожнистої кулі (одна восьма, або сегмент 45?? порожнистої півкулі)
- Внутрішній радіус сфери = 2 дюйми
- Зовнішній радіус сфери = 4 дюйми
- Товщина стінки = 2 дюйма
Параметри сітки
- Тип сітки = суцільна, чотиригранна
- Порядок елементів = Параболічний
- Розмір сітки = 0,333 дюйма, абсолютний
- Адаптивне уточнення сітки: немає
Властивості матеріалу
- Модуль пружності = 3,0 X 107 psi
- Щільність = 0,284 фунта маси/дюйм3
- Коефіцієнт Пуассона (v) = 0,29
- Межа текучості = 36 000 psi
- Нелінійний тип = пластик
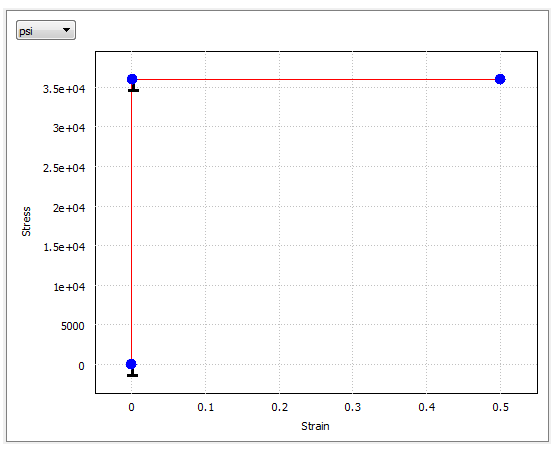
- Дані про напругу-деформацію:
| Процідити | Напруга ? psi (кПа) |
|---|---|
| 0,0 | 0,0 |
| 0,0012 | 36 000 (248 211) |
| 0,5 | 36 000 (248 211) |
обмеження
- Структурне обмеження без тертя на кожній із трьох плоских поверхонь
навантаження
- Перехідний тиск, прикладений до внутрішньої сферичної поверхні
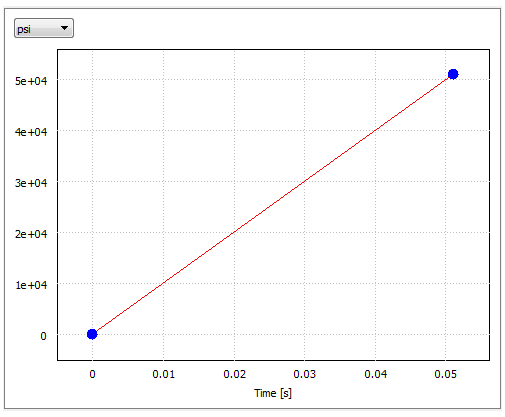
- Дані мультиплікаційної кривої (тиск зростає на 1000 фунтів/кв. дюйм на мілісекунду):
| час | Величина |
|---|---|
| 0,0 | 0,0 |
| 0,051 | 51 000 |
Теоретичні результати
Ми розглядаємо рішення для двох граничних випадків, коли пластичність прогресує від внутрішньої поверхні до зовнішньої поверхні:
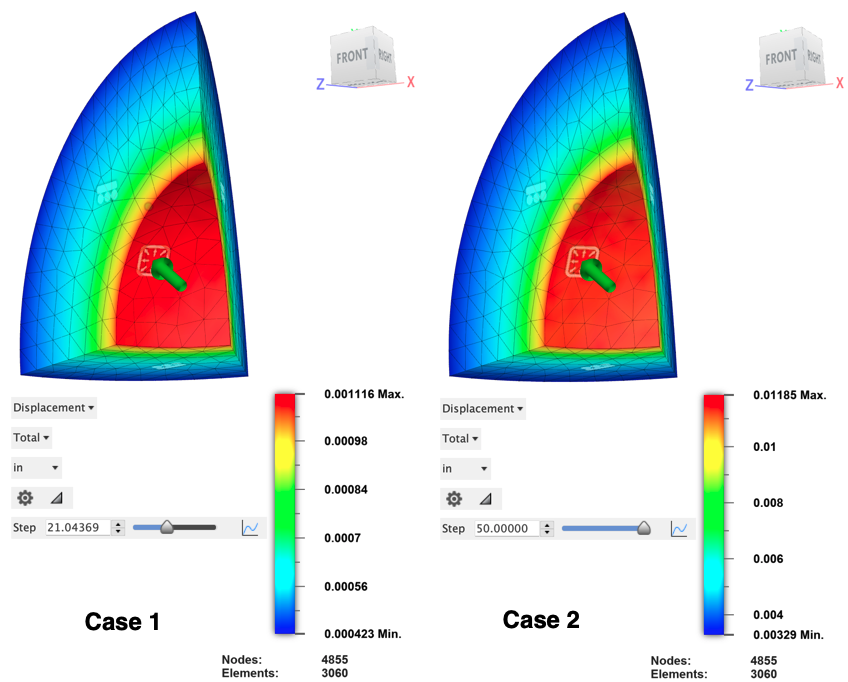
- Випадок 1 (початок пластичності), коли внутрішня поверхня просто стає пластичною
- Випадок 2 (100% проникнення пластику), в якому зовнішня поверхня просто стає пластиком
Ми обчислюємо дві змінні: радіальне зміщення внутрішньої поверхні (?i) у дюймах і прикладений тиск (P) у psi.
Корпус 1 (просто пластиковий)
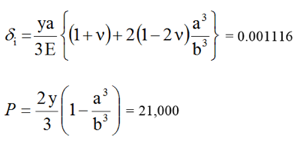
Корпус 2 (100% пластик)
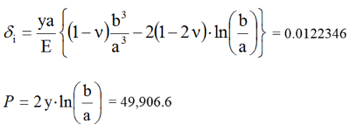
Де:
- y = 36 000 psi (межа текучості матеріалу)
- E = 30 x 106 psi (модуль Юнга)
- ? = 0,29 (коефіцієнт Пуассона)
- a = 2 in (внутрішній радіус сфери)
- b = 4 in (зовнішній радіус сфери)
Порівняння результатів
Fusion 360 інтерполює результати між вихідними кроками розв’язувача. Тиск, при якому модель щойно досягає рівня напруги 36 000 фунтів на квадратний дюйм, можна визначити за допомогою двовимірної діаграми максимальних результатів напруги по фон Мізесу. Якомога точніше знайдіть точку на графіку, де рівень напруги вперше досягає 36 000 psi. Збільште масштаб для кращої роздільної здатності під час перетягування перехрестя над графіком. Щоб збільшити масштаб, натисніть і перетягніть критичну частину графіка. Крок випадку 1 становить приблизно 21,94. Тиск збільшується на 1000 psi за крок, але крок нульового тиску дорівнює 1, а не 0. Тому прикладений тиск для випадку 1 = (21,94 – 1) * 1000 psi = 20 940 psi.
Відобразіть результати загального об’єму для того самого кроку. Через геометрію всі зміщення є радіальними, а максимальне зміщення відбувається на внутрішній поверхні протягом усієї події.
Тиск, при якому досягається повна пластичність, визначається шляхом перегляду 2D діаграми результатів максимального загального об’єму. Визначити крок, на якому максимальне переміщення знаходиться на межі швидкого зростання. (Якщо досягнуто повної пластичності, ніщо не завадить швидкому розширенню сфери.) Ця умова виникає приблизно на кроці 51.00. До цього кроку переміщення збільшується дуже поступово. Починаючи з кроку 51,0001 і вище, швидкість зміни помітно збільшується. Отже, прикладений тиск для випадку 2 = (52 – 1) * 1000 фунтів на квадратний дюйм = 50 000 фунтів на квадратний дюйм, а легенда графіка показує відповідне переміщення.
| Номер справи | Прикладений тиск (psi): | Радіальне зміщення (дюйми): | ||||
|---|---|---|---|---|---|---|
| Теорія | Fusion 360 | % різниці | Теорія | Fusion 360 | % різниці | |
| 1 | 21 000 | 20 940 | -0,29 % | 0,001116 | 0,001108 | -0,72 % |
| 2 | 49 906,6 | 50 000 | 0,19 % | 0,0122346 | 0,01184 | -3,23 % |
довідка
Чакрабарті, Дж., Теорія пластичності , McGraw-Hill, Нью-Йорк, 1987, сторінки 307-311.
Орігінал сторінки: Event Simulation 01