Дослідіть базову теорію, що лежить в основі дослідження моделювання подій.

Симуляції подій поєднують принципи закону Гука (F=-kx) і 2-го закону Ньютона (F=ma). Після об’єднання цих двох рівнянь шляхом виключення силового члена ми отримуємо ma + kx = 0. Тепер ми можемо додати ефекти демпфування (F=-cv), щоб отримати загальне рівняння руху:

ma+cv+kx = 0

де m — маса, a — прискорення, c — коефіцієнт демпфування, v — швидкість, k — жорсткість, x — переміщення. У матричній формі це рівняння представлено у вигляді:

[M]{a} + [C]{v}+[K]{x} = 0

З цього основного рівняння можна визначити напруги та деформації за допомогою вектора зміщення {x} та основних законів, що керують реакцією матеріалу.

Інтегрування часу за центральною різницею

Симуляція подій використовує явний розв’язувач, побудований на алгоритмі інтеграції центральної різниці в часі. Цей алгоритм використовує знання двох попередніх станів для безпосереднього визначення поточного стану (переміщення, швидкості та прискорення). Розмір кроку в часі від одного стану до наступного визначається стабільним приростом часу, також відомим як межа стабільності Куранта. Стабільний приріст часу регулює найбільший допустимий крок часу, після якого рішення вибухне. Якщо розглядати вплив демпфування, це виражається як:

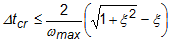
Де? tcr — стабільний приріст часу, ?max — найбільша власна частота в сітці, а ? – частка критичного демпфування в найвищому режимі.

Загалом, стабільні прирости часу в симуляції події дуже малі. Хороша новина полягає в тому, що явний розв’язувач дуже ефективний і може з відносною легкістю обробляти нелінійності матеріалу та контакту, оскільки на кожній ітерації не потрібно формувати матрицю жорсткості. Вузлові прискорення можна вирішити безпосередньо.